Hyper-Null Models and Their Applications

Abstract

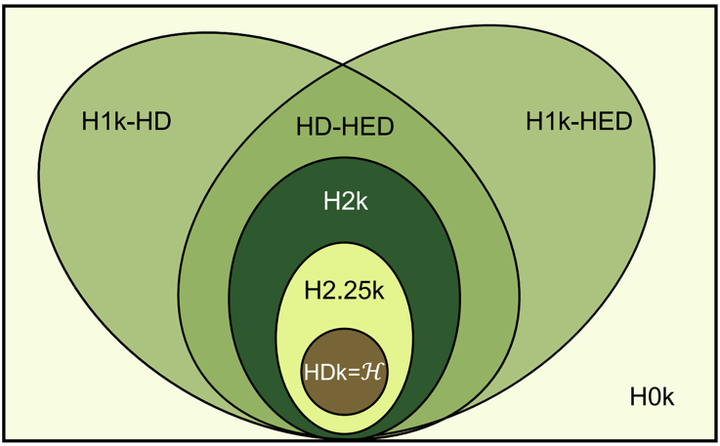
Null models are crucial tools for investigating network topological structures. However, research on null models for higher-order networks is still relatively scarce. In this study, we introduce an innovative method to construct null models for hypergraphs, namely the hyperedge swapping-based method. By preserving certain network properties while altering others, we generate six hyper-null models with various orders and analyze their interrelationships. To validate our approach, we first employ hypergraph entropy to assess the randomness of these null models across four datasets. Furthermore, we examine the differences in important statistical properties between the various null models and the original networks. Lastly, we investigate the impact of hypergraph randomness on network dynamics using the proposed hyper-null models, focusing on dismantling and epidemic contagion. The findings show that our proposed hyper-null models are applicable to various scenarios. By introducing a comprehensive framework for generating and analyzing hyper-null models, this research opens up avenues for further exploration of the intricacies of network structures and their real-world implications.

Yujie Zeng

PhD Candidate

My research interests primarily focus on network science, higher-order network analysis, graph representation learning and interdisciplinary applications.

Linyuan Lü

Professor

Professor, doctoral supervisor, winner of the National Natural Science Foundation of Outstanding Youth Science Fund.